SISTEM PERSAMAAN LINIER TIGA VARIABEL
Persamaan linier tiga variabel, yaitu persamaan yang mengandung tiga variabel dengan pangkat tertinggi satu. Bentuk umumnya ax + by + cz + d = 0. Dalam hal ini a, b dan c masing-masing dinamakan koefisien dari x, y dan z, sedangkan d dinamakan konstanta.
Metoda menentukan himpunan penyelasaiannya adalah
(a) Metoda substitusi
(b) Metoda eliminasi
Namun dalam prakteknya kedua metoda itu dipakai bersamaan dalam satu soal. Untuk lebih jelasnya akan diuraikan pada contoh berikut ini :
01. Dengan metoda campuran, tentukanlah penyelesaian sistem persamaan linier :
x + 3y – 3z = –7
2x – 2y + z = 8
Metoda menentukan himpunan penyelasaiannya adalah
(a) Metoda substitusi
(b) Metoda eliminasi
Namun dalam prakteknya kedua metoda itu dipakai bersamaan dalam satu soal. Untuk lebih jelasnya akan diuraikan pada contoh berikut ini :
01. Dengan metoda campuran, tentukanlah penyelesaian sistem persamaan linier :
x + 3y – 3z = –7
2x – 2y + z = 8
2x + y + z = 5
Jawab

02. Dengan metoda campuran, tentukanlah penyelesaian sistem persamaan linier :
2x + y + 3z = 1
2x – 3y + 4z = –5
x + 2y – z = 7
Jawab
03. Dengan metoda campuran, tentukanlah penyelesaian sistem persamaan linier :
2x + 3y – 3z = 10
2x – y + 2z = 1
4x + 4y + z = 11
Jawab
Misalkan : 2x + 3y – 3z = 10 ...............................................(1)
2x – y + 2z = 1 .................................................. (2)
4x + 4y + z = 11 ................................................ (3)
Jawab

2x + y + 3z = 1
2x – 3y + 4z = –5
x + 2y – z = 7
Jawab
03. Dengan metoda campuran, tentukanlah penyelesaian sistem persamaan linier :
2x + 3y – 3z = 10
2x – y + 2z = 1
4x + 4y + z = 11
Jawab
Misalkan : 2x + 3y – 3z = 10 ...............................................(1)
2x – y + 2z = 1 .................................................. (2)
4x + 4y + z = 11 ................................................ (3)
sumber : http://materimatematikalengkap.blogspot.com/2017/10/sistem-persamaan-linier-tiga-variabel.html

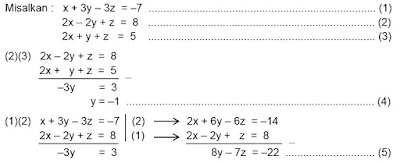















No comments:
Post a Comment